Temas
Recordemos que definimos a la función logaritmo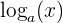 
como la función inversa del exponente 
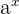. Por lo tanto, se cumple la relación
El número 
se conoce como base del exponente. Para más información, consulta nuestra página sobre los logaritmos.
Derivada del logaritmo natural
Si la base del logaritmo es el número de Euler, 
, entonces se logaritmo se conoce como logaritmo natural (o logaritmo neperiano). En este caso lo denotamos
Si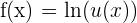 
, entonces la derivada del logaritmo natural es
donde ya estamos tomando en cuenta la regla de la cadena.
En particular, la derivada de 
es
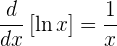
Derivada de un logaritmo de cualquier base
Sabemos que el logaritmo cumple con la siguiente propiedad:
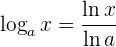
Por lo tanto, si derivamos la expresión anterior, tenemos:
Así, la derivada del logaritmo base 
es
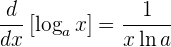
Si tomamos en cuenta la regla de la cadena, entonces la derivada es
Nota: en muchos casos es preferible aplicar algunas propiedades de los logaritmos antes de derivar. Por ejemplo, si tenemos
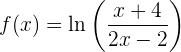
Entonces utilizamos la propiedad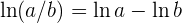 
para obtener:
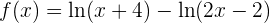
con lo que nos evitaríamos hacer la regla del cociente para las derivadas.
Ejercicios resueltos
1 Calcula la derivada de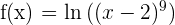 
Observemos que tenemos una potencia. Aunque es sencillo derivar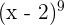 
, también podemos utilizar la siguiente propiedad de los logaritmos:
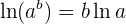
con lo que la función se puede escribir como
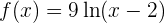
Entonces podemos derivar una expresión un poco más sencilla. Primero utilizamos la linealidad de la derivada (sacamos la constante):
ahora derivamos (con regla de la cadena donde 
):
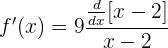
La derivada de 
es 1, por lo que tenemos
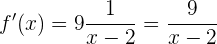
la cual es la derivada que buscábamos.
2 Calcula la derivada de
Antes de derivar, utilicemos la siguiente propiedad del logaritmo
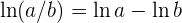
Por lo que la función se escribe como
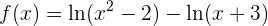
Ahora derivamos:
Utilizamos la linealidad de las derivadas:
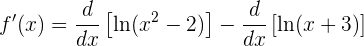
Y ahora derivamos cada expresión:
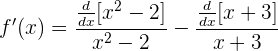
Luego, tenemos que 
y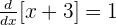 
, son lo que tenemos
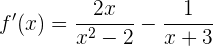
que es la derivada que buscamos.
3 Calcula la derivada de
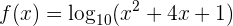
Recordemos que la derivada de un logaritmo con base diferente de es ligeramente diferente. Por lo tanto,
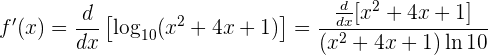
Además, tenemos que 
. Por lo que la derivada es
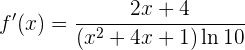
4 Calcula la derivada de
Para encontrar esta derivada, primero vale la pena utilizas propiedades de los logaritmos. En primer lugar
como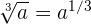 
, entonces la función se puede escribir como
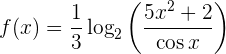
Ahora, utilizamos la propiedad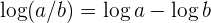 
, para escribir la función como
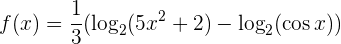
Ya podemos derivar la función:
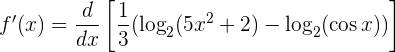
Utilizamos la linealidad de la derivada:
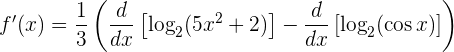
Ahora sí derivamos cada expresión:
Luego, tenemos que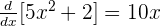 
y 
. Sustituyendo, tenemos
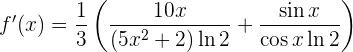
que es la derivada que buscábamos.
5 Utilizando derivación implícita y el hecho de que
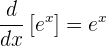
demuestra que
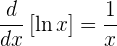
Empezamos con nuestra función . Deseamos mostrar que
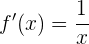
Para esto, aplicamos la función exponencial a ambos lados:
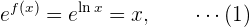
Ahora, usamos derivación implícita en esta expresión
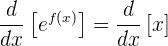
El lado derecho es
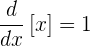
Mientras que el lado izquierdo es
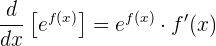
Por lo tanto, tenemos
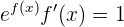
Si dividimos ambos lados por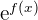 
, tenemos
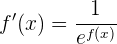
Sin embargo, teníamos que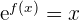 
en (1), por lo que
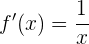
que era justo lo que queríamos demostrar.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4