Temas

Ejercicios del teorema de Rolle
1Estudiar si se verifica el teorema de Rolle en el intervalo 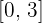 de la función:
de la función:

1 En primer lugar comprobamos que la función es continua en  . Para ello calculamos los límites laterales
. Para ello calculamos los límites laterales
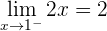
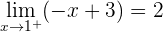
Como los límites laterales son iguales, entonces  .
.
Calculamos  . Como el límite en
. Como el límite en  coincide con su evaluación, entonces la función es continua en
coincide con su evaluación, entonces la función es continua en  .
.
2 En segundo lugar comprobamos si la función es derivable en  , para esto derivamos la función
, para esto derivamos la función

Como 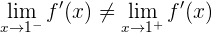 , entonces concluimos que la función no es derivable en
, entonces concluimos que la función no es derivable en  , luego la función no es derivable en el intervalo
, luego la función no es derivable en el intervalo  y por tanto no se cumple el teorema de Rolle.
y por tanto no se cumple el teorema de Rolle.
2¿Es aplicable el teorema de Rolle a la función  en el intervalo
en el intervalo 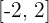 ?
?
1 En primer lugar calculamos el dominio de la función

2 La función es continua en el intervalo 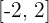 y derivable en
y derivable en  , porque los intervalos están contenidos en
, porque los intervalos están contenidos en 
Además se cumple que  , por tanto es aplicable el teorema de Rolle.
, por tanto es aplicable el teorema de Rolle.
3Comprobar que la ecuación 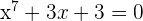 tiene una única solución real.
tiene una única solución real.
1 Como se trata de un polinomio, entonces la función es continua y derivable en todo 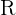
2 Verificamos el teorema de Bolzano en el intervalo  , para ello evaluamos en los extremos el intervalo
, para ello evaluamos en los extremos el intervalo
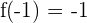 y
y  , por tanto es aplicable el teorema de Bolzano y se tiene que existe una raiz en el intervalo
, por tanto es aplicable el teorema de Bolzano y se tiene que existe una raiz en el intervalo  .
.
3 Verificamos el teorema de Rolle, para ello derivamos la función

Como la derivada no se anula en ningún valor (siempre es positiva) está en contradicción con el teorema de Rolle, por tanto sólo tiene una raíz real.
Ejercicio del teorema de Lagrange
4¿Se puede aplicar el teorema de Lagrange a 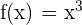 en
en 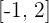 ?
?
1 Verificamos que la función sea continua en el intervalo  lo cual se cumple ya que la función es polinomial.
lo cual se cumple ya que la función es polinomial.
2 Verificamos que la función sea derivable en el intervalo  lo cual se cumple ya que
lo cual se cumple ya que 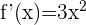 es polinomial
es polinomial
3 Se cumplen las hipótesis del teorema de Lagrange, por lo que existe  tal que
tal que
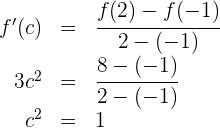
Obtenemos los valores 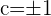 . Tomamos
. Tomamos 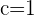 , ya que
, ya que  y observamos que
y observamos que 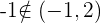 .
.
Ejercicio del teorema de Cauchy
5Comprobar si se cumplen las hipótesis del teorema de Cauchy para las funciones 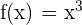 y
y  en el intervalo
en el intervalo  .
.
1 Las funciones  y
y  son continuas en el intervalo
son continuas en el intervalo  y derivables en
y derivables en  , por ser funciones polinómicas.
, por ser funciones polinómicas.
2 Se cumple que 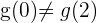 , por lo tanto se verifica el teorema de Cauchy
, por lo tanto se verifica el teorema de Cauchy
3 Calculamos las derivadas de las funciones
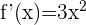
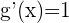
4 Evaluamos en la fórmula del teorema de Cauchy
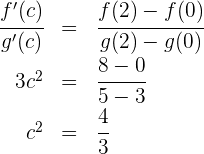
Las raíces son 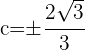
5 Tomamos 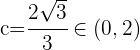 , ya que
, ya que 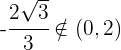
Como 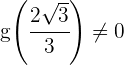 , concluimos que el valor buscado es
, concluimos que el valor buscado es 
Ejercicios de la regla de L'Hôpital
Resolver los siguientes límites:
¿Vives en la capital andaluza? ¡No te pierdas nuestras clases particulares matematicas Sevilla!
6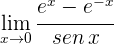
1 Evaluando  se obtiene la indeterminación
se obtiene la indeterminación
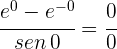
2 Derivamos el numerador y el denominador
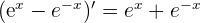

3 Aplicamos la regla de L'Hôpital
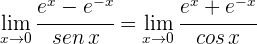
4 Resolvemos el límite obtenido

7
1 Para 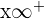 se obtiene la indeterminación
se obtiene la indeterminación 
2 Derivamos el numerador y el denominador
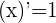
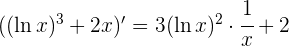
3 Aplicamos la regla de L'Hôpital

4 Aplicamos nuevamente la regla de L'Hôpital al elemento del denominador

5 Aplicamos nuevamente la regla de L'Hôpital

6 Así, el límite es
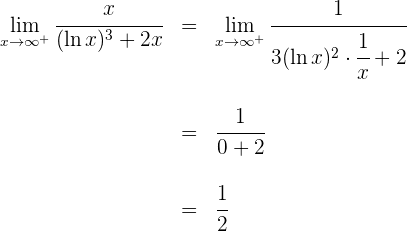
Si buscas clases particulares de matematicas Madrid, ¡prueba las de Superprof!
8
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 
2 Sumamos las fracciones
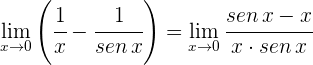
Para  se obtiene la indeterminación
se obtiene la indeterminación 
3 Calculamos las derivadas
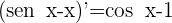
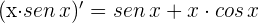
4 Aplicamos la regla de L'Hôpital

Para  se obtiene la indeterminación
se obtiene la indeterminación 
5 Aplicamos nuevamente la regla de L'Hôpital
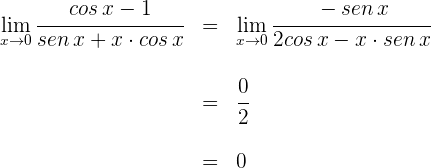
9
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 
2 Calculamos las derivadas
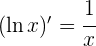

3 Aplicamos la regla de L'Hôpital

10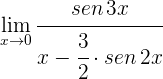
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 
2 Calculamos las derivadas
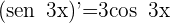
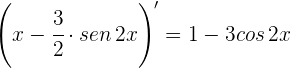
3 Aplicamos la regla de L'Hôpital
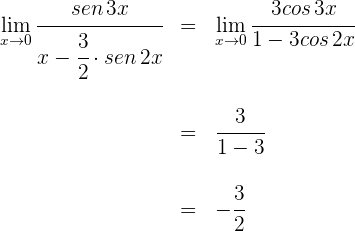
11
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 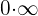
2 Escribimos 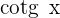 en términos de senos y cosenos
en términos de senos y cosenos

Para  se obtiene la indeterminación
se obtiene la indeterminación 
3 Calculamos las derivadas
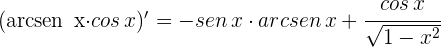

4 Aplicamos la regla de L'Hôpital

12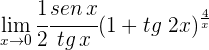
1 Escribimos  en términos de senos y cosenos; luego aplicamos límites
en términos de senos y cosenos; luego aplicamos límites
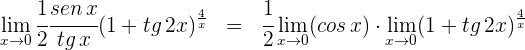
Como 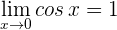 el límite se simplifica en
el límite se simplifica en

2 Para  se obtiene la indeterminación
se obtiene la indeterminación 
3 Escribimos 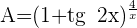 . Aplicando logaritmo natural y la exponencial obtenemos
. Aplicando logaritmo natural y la exponencial obtenemos

4 Escribimos nuevamente el límite y aplicamos que la función exponencial es continua
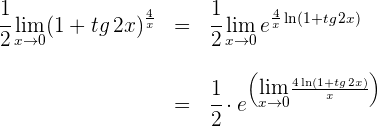
Ahora resta calcular
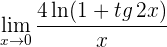
5 Para  se obtiene la indeterminación
se obtiene la indeterminación  . Calculamos las derivadas del numerador y denominador
. Calculamos las derivadas del numerador y denominador
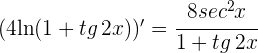
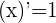
6 Aplicamos la regla de L'Hôpital
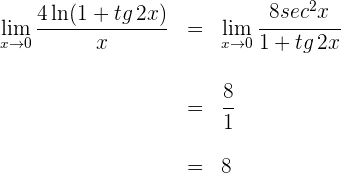
7 Así, el límite buscado es

13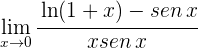
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 
2 Calculamos las derivadas

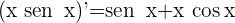
3 Aplicamos la regla de L'Hôpital

4 Para  se obtiene la indeterminación
se obtiene la indeterminación  , por lo que aplicamos de nuevo la regla de L'Hôpital
, por lo que aplicamos de nuevo la regla de L'Hôpital

14
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 
2 Calculamos las derivadas

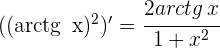
3 Aplicamos la regla de L'Hôpital

4 Para  se obtiene la indeterminación
se obtiene la indeterminación  , por lo que aplicamos de nuevo la regla de L'Hôpital
, por lo que aplicamos de nuevo la regla de L'Hôpital
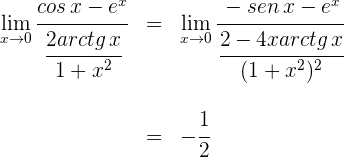
15
1 Para  se obtiene la indeterminación
se obtiene la indeterminación  . Realizamos la suma de fracciones
. Realizamos la suma de fracciones

Para  se obtiene la indeterminación
se obtiene la indeterminación  .
.
2 Calculamos las derivadas
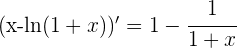
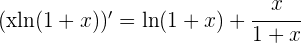
3 Aplicamos la regla de L'Hôpital
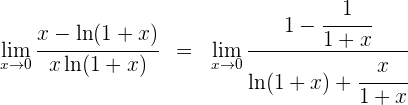
4 Para  se obtiene la indeterminación
se obtiene la indeterminación  , por lo que primero simplificamos y luego aplicamos de nuevo la regla de L'Hôpital
, por lo que primero simplificamos y luego aplicamos de nuevo la regla de L'Hôpital
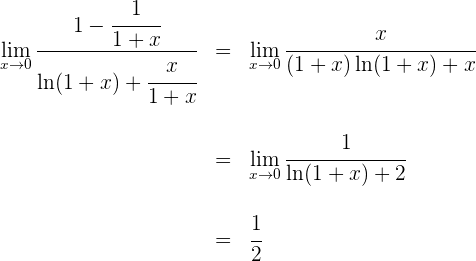
16
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 
2 Escribimos el límite empleando logaritmo natural y la exponencial
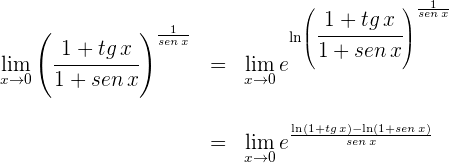
3 Escribimos nuevamente el límite y aplicamos que la función exponencial es continua
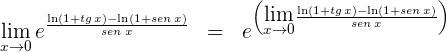
Ahora resta calcular
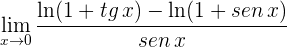
4 Para  se obtiene la indeterminación
se obtiene la indeterminación  . Calculamos las derivadas del numerador y denominador
. Calculamos las derivadas del numerador y denominador


5 Aplicamos la regla de L'Hôpital

6 Así, el límite buscado es
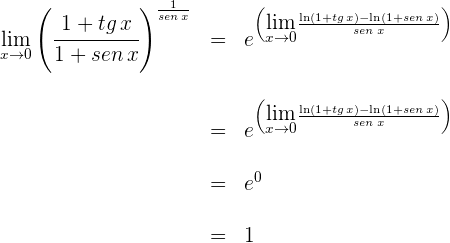
17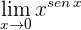
1 Para  se obtiene la indeterminación
se obtiene la indeterminación 
2 Escribimos el límite empleando logaritmo natural y la exponencial

3 Escribimos nuevamente el límite y aplicamos que la función exponencial es continua

Ahora resta calcular
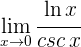
4 Para  se obtiene la indeterminación
se obtiene la indeterminación  . Calculamos las derivadas del numerador y denominador
. Calculamos las derivadas del numerador y denominador
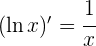

5 Aplicamos la regla de L'Hôpital

Para  se obtiene la indeterminación
se obtiene la indeterminación  . Aplicamos nuevamente la regla de L'Hôpital
. Aplicamos nuevamente la regla de L'Hôpital

6 Así, el límite buscado es














Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4